已知条件：

圆盘的质量 M 为50公斤，
圆盘的直径 D 为500毫米，
圆盘所能达到的最高转速为60转每分钟。
请根据这些信息，选择适合的伺服电机及减速机，并参考以下构件示意图进行选型。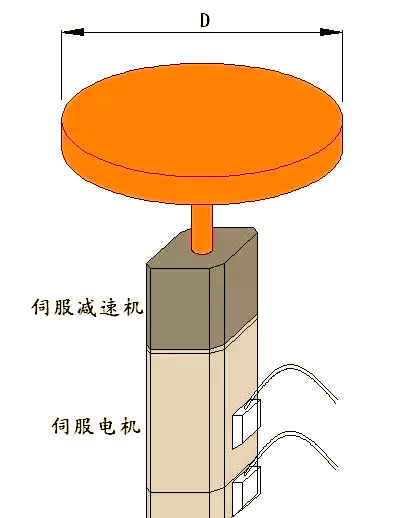

计算圆盘的转动惯量

JL = MD²/8 = 50 * 50²/8 = 15625 kg·cm²

设减速机的减速比为1:R，则伺服电机轴上的负载惯量为15625/R²。

根据负载惯量小于3倍电机转子惯量 JM 的原则
若选择400W电机，其转子惯量 JM = 277 kg·cm²，则需满足 15625/R² < 3*277，即 R² > 18803，R > 137。但这样会导致输出转速过低，无法满足要求。

若选择500W电机，其转子惯量 JM = 17 kg·cm²，则需满足 15625/R² < 3*17，即 R² > 637，R > 25。这样的减速比对应的输出转速为2000/25=80rpm，满足要求。

此外，这种传动方式的阻力非常小，可以忽略扭矩计算。

案例

已知条件：

负载重量 M = 50 kg，
同步带轮直径 D = 120 mm，
减速比 R1 = 10，R2 = 2，
负载与机台摩擦系数 µ = 6，
负载最高运动速度为 30 m/min，
负载从静止加速到最高速度所需时间为200ms，
忽略各传送带轮的重量。

试求：驱动此类负载所需的最低电机功率。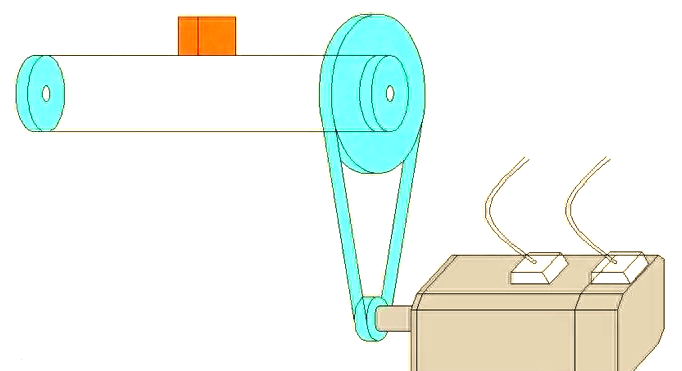

计算折算到电机轴上的负载惯量：
JL = M * D² / 4 / R1²
= 50 * 144 / 4 / 10= 18 [kg·cm²]

根据负载惯量小于3倍电机转子惯量JM的原则
我们得出：
JM > 6 [kg·cm²]

计算电机驱动负载所需要的扭矩：
克服摩擦力所需转矩Tf = M * g * µ * (D/2) / R2 / R= 50 * 8 * 6 * 06 / 2 / = 882 [N·m]

加速时所需转矩Ta = M * a * (D/2) / R2 / R= 50 * (30 / 60 / 2) * 06 / 2 / = 375 [N·m]

因此，伺服电机的额定转矩应大于Tf，最大扭矩应大于Tf + Ta。

计算电机所需要的转速：
N = v / (πD) * R= 30 / (14 * 12) * = 796 [rpm]

案例已知：

负载重量 M=200 kg，
螺杆螺距 PB=20 mm，
螺杆直径 DB=50 mm，
螺杆重量 MB=40 kg，
摩擦系数 µ=2，
机械效率 η=9，
负载移动速度 V=30 m/min，
全程移动时间 t=4 s，
加减速时间 t1=t3=2 s，
静止时间 t4= 3 s。

请选择能够满足负载需求的最小功率伺服电机。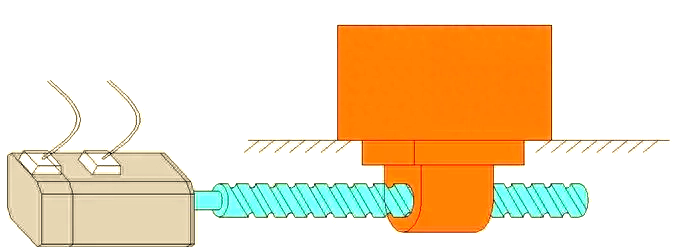

计算折算到电机轴上的负载惯量
重物折算到电机轴上的转动惯量 JW = M * (PB / 2π)^2 = 200 * (2/28)^2 = 29 kg·cm^螺杆转动惯量 JB = MB * DB^2 / 8 = 40 * 25 / 8 = 125 kg·cm^总负载惯量 JL = JW + JB = 129 kg·cm^
计算电机转速
电机所需转速 N = V / PB = 30 / 02 = 1500 rpm

计算电机驱动负载所需要的扭矩
克服摩擦力所需转矩 Tf = M * g * µ * PB / (2π * η) = 200 * 8 * 2 * 02 / (2π * 9) = 387 N·m
重物加速时所需转矩 TA1 = M * a * PB / (2π * η) = 200 * (30/60/2) * 02 / (2π * 9) = 769 N·m
螺杆加速时所需转矩 TA2 = JB * α / η = JB * (N * 2π / 60 / t1) / η = 0125 * (1500 * 28 / 60 / 2) / 9 = 903 N·m
加速所需总转矩 TA = TA1 + TA2 = 672 N·m

选择伺服电机
伺服电机额定扭矩 T > Tf 且 T > Trms（此处未给出Trms值，需根据实际情况确定）
伺服电机最大扭矩 Tmax > Tf + TA
最后选定ECMA-E31820ES电机。